Débit d’un écoulement :
Le débit d’un écoulement est le quotient du volume de liquide écoulé par la durée de cet écoulement. C’est donc la quantité de liquide qui s’écoule en une unité de temps.
Unité usuelle : m3 /s. On mesure aussi en L /min.
Exemple : Le débit de la Loire à Nantes est en moyenne 650 m3 /s.
Décagone :
Un décagone est un polygone qui a dix côtés. 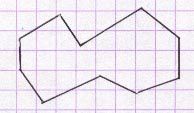
Décamètre :
Un décamètre représente dix mètres.
Symbole : dam.
Décimètre :
Un décimètre est un dixième de mètre.
Symbole : dm.
Déduire :
Déduire, c’est utiliser les résultats ou les conclusions précédentes pour obtenir le résultat ou la conclusion demandée.
Définition :
Une définition est une phrase qui caractérise un être mathématique.
Degré :
Le degré est une unité usuelle de mesure d’angle.
Symbole : °.
Exemple : Un angle droit mesure 90°.
Demi-cercle :
Un demi-cercle est une partie d’un cercle limitée par deux points diamétralement opposés. 
Demi-droite :
Une demi-droite est une partie de droite limitée dans un sens par un point appelé origine, illimitée dans l’autre sens. 
Notation : [AB) est la demi-droite d’origine A passant par B.
Demi-plan :
Un demi-plan est une région du plan limitée par une droite. 
Démonstration :
La démonstration est l’action de démontrer. C’est donc l’ensemble du raisonnement qui sert à prouver qu’une propriété est vraie.
Démontrer :
Démontrer, c’est prouver une propriété.
On se base sur des hypothèses, on utilise des définitions ou des propriétés du cours pour arriver à une conclusion.
Dénominateur :
Le dénominateur d’un quotient ou d’une fraction a / b (b ≠ 0) est le nombre b.
Exemple : 5 est le dénominateur de la fraction 3 / 5.
Descartes :
René Descartes, originaire de la Touraine, est un grand philosophe et mathématicien du 17ème siècle (1596-1650).

Il est à l’origine de la géométrie analytique et invente en particulier un système de coordonnées. Son nom reste lié aux coordonnées cartésiennes.
Descartes pense que tous les problèmes peuvent être résolus par les mathématiques, il suffit pour cela de les mettre en équation et de les résoudre.
Déterminer :
Déterminer, c’est trouver des éléments mathématiques (numériques ou géométriques) justifiant les calculs ou les raisonnements.
Deux :
Deux est un chiffre qui s’écrit 2.
Exemple : Nous avons deux yeux.
Développement :
Le développement est l’action de développer une expression.
Développer :
Développer une expression littérale, c’est supprimer ses parenthèses en respectant certaines règles.
Règles : a + (b + c) = a + b + c
a + (b - c) = a + b - c
a - (b + c) = a - b - c
a - (b - c) = a - b + c
a (b + c) = ab + ac
a (b - c) = ab – ac
(a + b)(c + d) = ac + ad + bc + bd
Exemples :
(5x + 2) + (4x – 1) = 5x + 2 + 4x – 1 = 9x + 1.
(6x² + 3x + 9) – (2x² + x + 2) = 6x² + 3x + 9 – 2x² – x – 2 = 4x² + 2x + 7.
4(3x + 5) = 12x + 20.
7(4x + 9) – 3(2x – 4) = 28x + 63 – 6x + 12 = 22x + 75.
(3x + 2)(4x – 1) = 12x² – 3x + 8x – 2 = 12x² + 5x – 2.
Diagonale d’un parallélépipède rectangle :
Une diagonale d’un parallélépipède rectangle est un segment reliant deux sommets d’un parallélépipède rectangle n’appartenant pas à la même face.
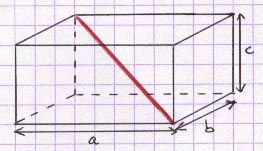
La longueur de chacune des quatre diagonales d’un parallélépipède rectangle de dimensions a, b et c est √(a² + b² + c²).
Dans le cas particulier d’un cube d’arête a, la longueur de la diagonale est a√3.




















