Distance à zéro :
La distance à zéro (ou valeur absolue) d’un nombre relatif est sa partie numérique.
Exemple : La distance à zéro de – 3 est 3.
La distance à zéro de 5,4 est 5,4.
Distance d’un point à une droite :
La distance d’un point A à une droite Δ est la distance du point A au point H de la droite Δ tel que (AH) est perpendiculaire à Δ. 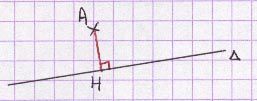
d (A , Δ) = AH.
Distance entre deux points :
La distance entre deux points A et B est le nombre d’unités de longueur qu’il y a entre A et B.
Notation : AB ou d (A,B).
 AB = 4 cm.
AB = 4 cm.
Dans un repère orthonormal, si A (xA ; yA) et B (xB ; yB) ,
alors AB = √[(xB - xA)² + (yB - yA)²].
Exemple : Dans un repère orthonormal d’unité 1 cm, on a : C ( -2 ; 5) ; D ( 3 ; 4) .
Calculer la distance CD.
C (-2 ; 5) ; D (3 ; 4)
CD = √[(3 + 2)² + (4 - 5)² ]
CD = √[5² + (- 1)²]
CD = √(25+ 1)
CD = √26.
Distinct :
Deux points sont distincts s’ils ne sont pas confondus.

Distributivité :
La multiplication est distributive par rapport à l’addition.
Pour tous nombres a, b et c : a(b + c) = ab + ac.
Exemple : 7 ×(9 + 1) = 7 × 9 + 7 × 1 = 63 + 7 = 70.
7 ×(9 + 1) = 7 × 10 = 70.
La multiplication est distributive par rapport à la soustraction.
Pour tous nombres a, b et c : a(b – c) = ab – ac.
Exemple : 8 ×(12 – 2) = 8 × 12 – 8 × 2 = 96 – 16 = 80.
8 ×(12 – 2) = 8 × 10 = 80.
Dividende :
Un dividende est un nombre entier qui va être divisé dans une division euclidienne.
 a est le dividende.
a est le dividende.
Exemple :
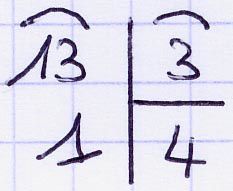
13 est le dividende.
Diviseur :
Un diviseur est un nombre entier par lequel on divise dans une division euclidienne.

b est le diviseur.
Exemple : 
4 est le diviseur.
Si a et b sont des entiers, on dit que b est un diviseur de a s’il existe un nombre entier q tel que
a = b × q.
Exemple : 5 est un diviseur de 30 car 30 = 6 × 5.
Divisible :
a et b étant des entiers, on dit que a est divisible par b si b est un diviseur de a.
Exemple : 40 est divisible par 8 car 40 : 8 = 5 ou 40 = 8 × 5.
Voir critère de divisibilité.
Division :
Une division est une opération qui à deux nombres a et b associe leur quotient a : b.
Exemple : 45 : 9 = 5.
Technique :
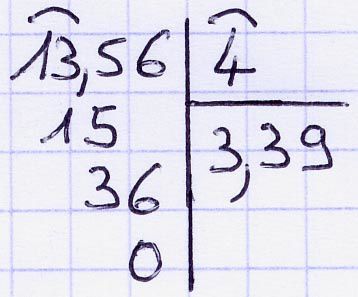
donc 13,56 : 4 = 3,39.
Division des fractions :
Pour effectuer une division de fractions, on multiplie la première fraction par l’inverse de la seconde.
Si a, b, c et d sont des entiers tels que b ≠0, c ≠0 et d ≠ 0, :
(a / b) : (c / d) = (a / b) × (d / c) = (a × d) / (b × c) .
Exemple : (2 / 3) : (5 / 7) = (2 / 3) × (7 / 5) = 14 / 15.
Division des nombres relatifs :
Pour effectuer une division de nombres relatifs, on divise leurs parties numériques et on applique la règle des signes suivante :
Si les deux nombres sont de même signe, leur quotient est positif .
Sinon, leur quotient est négatif.
Exemple : - 8 : ( - 2) = 4.
36 : (- 4) = - 9.
Division euclidienne :
Une division euclidienne est une division entre nombres entiers.
Elle est du type  où a, b, q et r sont des entiers (r < b).
où a, b, q et r sont des entiers (r < b).
a est le dividende, b est le diviseur, q est le quotient, r est le reste.
On a l’égalité euclidienne associée : a = b × q + r.
Exemple :
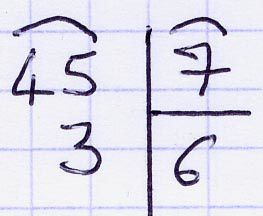
45 = 7 × 6 + 3 est l’égalité euclidienne associée.
Division exacte :
Une division exacte est une division où le reste est nul.
Exemple :
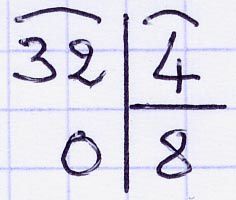
Division par 10, 100 ou 1000 :
Pour effectuer une division d’un nombre par 10, 100 ou 1000, on décale la virgule du nombre respectivement de 1, 2 ou 3 rangs vers la gauche.
Exemples : 364 : 100 = 3,64.
587,2 : 10 = 58,72.
Division par 0,1 ; 0,01 ou 0,001 :
Pour effectuer une division d’un nombre par 0,1 ; 0,01 ou 0,001, on décale la virgule respectivement de 1, 2 ou 3 rangs vers la droite.
Cela revient à multiplier par 10 ; 100 ou 1000.
Exemple : 8,4 : 0,01 = 8,4 × 100 = 840.
Dix :
Dix est un nombre qui s’écrit 10.
C’est la base de notre système décimal.
Exemple : Nos deux mains contiennent dix doigts.
Dizaine :
Une dizaine est un groupe de dix unités.
Dodécagone :
Un dodécagone est un polygone qui a douze côtés.