Isaac NEWTON (1642 – 1727), anglais :

Philosophe et mathématicien anglais, Isaac Newton sera un véritable précurseur.

Passionné par l’alchimie toute sa vie, il émet des idées sur l’origine de la Terre et son évolution.  

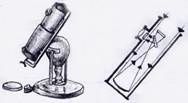
 Il s’intéressera aussi à l’optique. On lui doit l’invention du télescope qui porte son nom.  

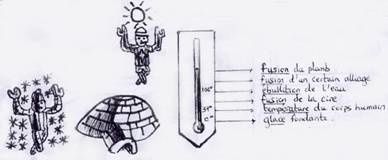
Newton donne la théorie mathématique de la transmission du son et construit un thermomètre ayant 6 points fixes…  

Il prouve que l’air est pesant en le comprimant dans une boule creuse.

Il étudie la dispersion de la lumière blanche par le prisme : chaque couleur a un caractère spécifique et inaltérable !

Newton découvre la loi de l’attraction universelle, les corps sont attirés vers le sol ! 

Les planètes s’attirent en fonction de leurs masses et de leurs distances.

  Il établit une formule permettant de calculer les mouvements de deux planètes à partir de leur vitesse, de leur distance et de leur masse. Cela lui permet d’expliquer les équinoxes ou les marées.

Voici des applications de la formule du binôme de Newton :

(a + b)² = a² + 2ab + b²   ;

(a + b) ³ = a³ + 3a²b + 3ab² + b³   ;

(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴.  

Newton est considéré, avec Leibniz, comme le fondateur du calcul infinitésimal : calcul différentiel (partie où on détermine les infiniment petits à l’aide de fonctions) et intégral (partie où on détermine des aires ou des fonctions à l’aide d’infiniment petits). Il le créera, mais poussera moins loin la formalisation que Leibniz.

Ses travaux sur les fonctions et les courbes sont aussi très importants. Il semble être le premier à introduire les coordonnées négatives dans un repère.

William HAMILTON (1805 – 1865), irlandais :

William Hamilton, grand mathématicien et physicien irlandais, enseigna l’astronomie à Dublin dès l’âge de 22 ans.

A 32 ans, Sir Hamilton était président de l’Académie royale d’Irlande.

On dit qu’à 5 ans, il lit le latin, le grec et l’hébreu. On prétend qu’à 13 ans, il parle 13 langues. A 17 ans, il publie ses premiers travaux.

Dès 25 ans, il écrit une théorie sur les nombres complexes, donnant une traduction des déplacements du plan à l’aide de l’addition et de la multiplication.

Les travaux d’Hamilton font référence à l’optique, à la dynamique, aux équations de degré 5 et aux équations différentielles.

Astronome royal à la cour d’Irlande, il invente les quaternions, genre de nombres qui caractérisent les éléments d’un espace à quatre dimensions.

 Il contribue aussi à la création du calcul vectoriel et de l’algèbre linéaire.

Il connaît, suite à l’échec de son mariage, quelques déboires et devient quelque peu alcoolique. Il meurt en 1865, à l’âge de 60 ans, de la goutte dans un état de misère physiologique avancé.

Evariste GALOIS (1811 – 1832), français :

 Evariste Galois est un mathématicien français né à Bourg-La-Reine en 1811.

A 15 ans, il étudie les travaux des grands mathématiciens.

A 18 ans, il publie ses premiers ouvrages (fractions, équations, racines carrées).

C’est à ce moment là qu’il découvre un critère pour résoudre des équations par des racines en développant la théorie des groupes.

Il présente alors son important travail à l’Académie des Sciences.

Il entre en 1829 à l’école normale mais se fait expulser en 1831 pour avoir reproché au directeur ses positions contre-révolutionnaires…

Pour des raisons politiques, à cause de ses propos républicains, il passe pratiquement ses derniers 18 mois en prison.  

Lors d’un duel, à 21 ans, il prend un coup de pistolet et meurt à l’hôpital Cochin en 1832.

Il rédige, pendant la nuit qui précède sa mort, une esquisse de ses conceptions mathématiques. Ses 60 pages ont une portée exceptionnelle sur les méthodes de résolution des équations où il développe considérablement la théorie des groupes. Il est le premier à prouver que l'on ne peut pas résoudre toutes les équations de degré 5 par des radicaux.

C’est seulement en 1870, 40 ans plus tard, que l’ampleur de ses travaux sera reconnue… La ‘‘théorie de Galois’’ a fait passer l’algèbre dans sa phase ‘‘moderne’’.

EUCLIDE (330 avant JC – 275 avant JC), grec : 

 Euclide est un savant grec qui enseignait les mathématiques à Alexandrie, en Egypte où il avait fondé la plus célèbre école de l’Antiquité.

L’œuvre d’Euclide est constituée en particulier des ‘‘Eléments’’, ensemble de 13 livres qui servent encore de modèle de nos jours à nos savants les plus illustres.

Cette œuvre est, après la Bible, celle qui a eu le plus d'éditions (plus de 800).

Les livres I, II, III, IV traitent uniquement de géométrie plane, le livre V de proportions et le livre VI des figures semblables. Les livres VII, VIII et IX sont consacrés à l'arithmétique et plus spécialement à la théorie des nombres, le livre X aux nombres transcendants. Les livres XI, XII et XIII parlent de géométrie dans l'espace avec les solides géométriques, les aires, les volumes et enfin les polyèdres réguliers.

Euclide y fait une synthèse de toutes les découvertes précédentes. Il y apporte lui-même des énoncés, des constructions, des définitions, des axiomes, des postulats, des propositions et des démonstrations. On y compte 130 définitions et 465 énoncés.

On retrouve les théorèmes de Thalès et de Pythagore, les solides de Platon, les polygones réguliers avec les cercles circonscrits et inscrits, etc… Pour Euclide, les nombres sont représentables par des segments, leur produit par des rectangles et la multiplication de trois entiers est représentée par un solide. Euclide fait presque toutes les démonstrations des résultats géométriques connus à son époque.

En géométrie, il reprend la démonstration de Pythagore qui prouve que la somme des angles d’un triangle est égale à 180°.  

Voici les cinq postulats (ou axiomes) d'Euclide :

1^er postulat :  "Par deux points, il passe une droite."

2^e postulat : "Tout segment peut être prolongé autant qu'on le souhaite."

3^e postulat : "De tout point, on peut tracer un cercle de n'importe quel rayon."

4^e postulat : "Tous les angles droits sont égaux."

5^e postulat : "Il existe une seule droite parallèle à d passant par A." 

En calcul, il nous laisse la division euclidienne et donc son égalité : 316 = 51 ×6 + 10. 

L’algorithme d’Euclide est un procédé qui permet de déterminer le P.G.C.D. (Plus Grand Commun Diviseur) de deux nombres entiers sans avoir à dresser la liste de leurs diviseurs.

Euclide nous a laissé une œuvre considérable qui a inspiré de nombreux autres mathématiciens, nous lui devons de nombreux résultats nouveaux, dans les ‘‘Eléments’’, mais aussi dans d’autres ouvrages. Son nom est attribué à de nombreux concepts mathématiques (axiome d’Euclide, division euclidienne, égalité euclidienne, espace euclidien, géométrie euclidienne, algorithme d’Euclide, anneau euclidien…).

Il a étudié la puissance visuelle de l'oeil et la propriété des miroirs plans.

Il s'est aussi posé la question de la forme de notre terre.

René DESCARTES (1596 – 1650), français :

René Descartes, originaire de la Touraine, est un grand philosophe et mathématicien français du XVII^ème siècle.

C’est dans son lit qu’il inventa les coordonnées cartésiennes, en regardant une mouche se déplaçant au plafond. C’est grâce à ce système que Descartes va créer la géométrie analytique (étude des figures par l’algèbre grâce à l’emploi de coordonnées).

Il caractérise les droites par leurs équations, résout les intersections des droites avec des systèmes d’équations. Il améliore les notations de Viète en choisissant a, b, c pour les quantités connues et x, y, z pour les inconnues, comme nous les utilisons dorénavant  (ax + by = c). Il sera le premier en 1637 à utiliser le mot ‘‘équation’’. Descartes découvrira aussi les principes de l’optique géométrique.

‘‘La Science devrait nous rendre maîtres et possesseurs de la nature’’ (Discours de la Méthode – Descartes). La grande idée de Descartes, c’est l’unité de la Science. Il présume que l’univers et tout ce qu’il contient doit obéir à des lois semblables. 

 Il pense que tous les problèmes peuvent être résolus par les mathématiques, il suffit pour cela de les mettre en équation et de les résoudre…

Descartes influencera le développement des sciences par son souci de la résolution d’un problème partie par partie et par celui de passer tout en revue afin de ne rien oublier. On dit de quelqu’un qu’il a un esprit cartésien s’il est méthodique et rationnel.