maths en dico - Le blog mathematique du professeur ROMETUS

16 janvier 2021 6 16 /01 /janvier /2021 17:57

Dictionnaire : de Stère à Système d'inéquations

Stère :

Un stère est une unité de mesure de volume utilisée pour le bois. C’est la quantité de bois correspondant à un volume extérieur d’un m³.

Symbole : st.

Suite d’opérations :

Une suite d’opérations est une succession d’opérations.

Exemple : 5 × 7 - 3 : 2 + 8.

Certaines opérations sont prioritaires par rapport à d’autres.

Suites proportionnelles :

Deux suites proportionnelles sont deux suites où il suffit de multiplier chacun des termes de la première suite par un même nombre non nul k pour obtenir les termes correspondants de la deuxième suite.

k est alors le coefficient de proportionnalité de la première suite à la seconde suite.

Exemple :

nombre de croissants	2	6
prix (€)	1,60	4,80

Le prix des croissants est proportionnel au nombre de croissants.

0,80 est leur coefficient de proportionnalité.

Supérieur :

Supérieur signifie : plus grand.

Notation : ≥ signifie : est supérieur ou égal à.

> signifie : est strictement supérieur à.

Exemple : 10,3 > 10,23.

Superposable :

Deux figures sont superposables lorsque le calque de l’une peut être posé exactement sur l’autre.

Exemple : L’image d’une figure par une symétrie orthogonale est une figure superposable.

Support :

Le support d’un segment ou d’une demi-droite est la droite qui contient ce segment ou cette demi-droite. S 24

La droite (AB) est le support du segment [AB].

Surface :

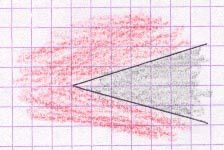
Une surface plane est une des régions déterminée par une figure géométrique (réalisée à partir des polygones, des cercles, des droites, etc...).

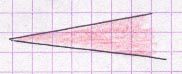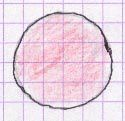secteur angulaire

(surface plane non mesurable)

disque

(surface plane mesurable)

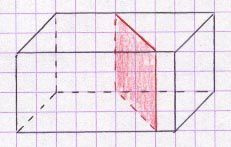
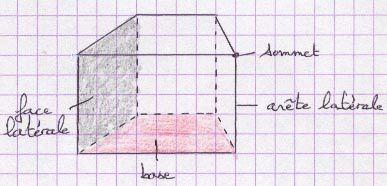
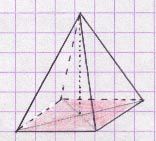
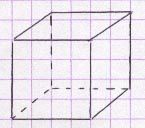
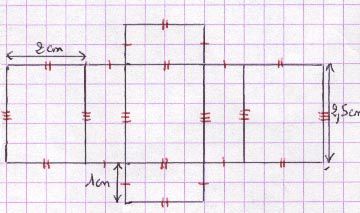
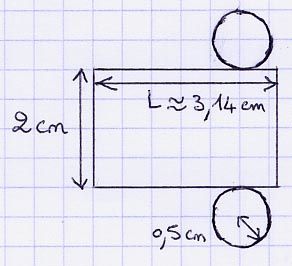
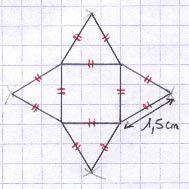
La surface d’un parallélépipède rectangle, d’un prisme droit ou d’une pyramide est celle de l’ensemble des faces extérieures qui composent ce solide.

La mesure d’une surface est une aire.

Sylvestre II :

Sylvestre II, Gerbert d’Aurillac, est né en France (938-1003).

En mathématiques, sa principale contribution a été d’introduire l’usage des chiffres indo-arabes en Europe.

Il est devenu pape en 999 sous le nom de Sylvestre II.

Symbole :

Un symbole est un caractère évitant d’écrire en toutes lettres les phrases mathématiques.

Exemple : d₁ ^ d₂ signifie d₁ est perpendiculaire à d₂.

^ est un symbole.

Quelques symboles usuels :

+ : plus Ï : n’appartient pas à

– : moins < : est strictement inférieur à

× : multiplié par ≤ : est inférieur ou égal à

: : divisé par > : est strictement supérieur à

= : est égal à ³ : est supérieur ou égal à

≠ : est différent de ^ : est perpendiculaire à

≈ : est environ égal à // : est parallèle à

Î : appartient à

Symétrie centrale :

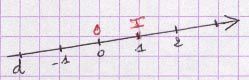
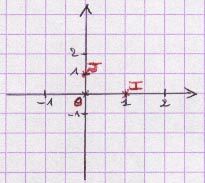
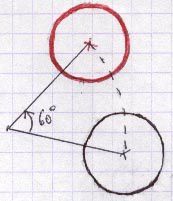
La symétrie centrale est la transformation qui associe à un point ou à une figure son symétrique par rapport à un point.

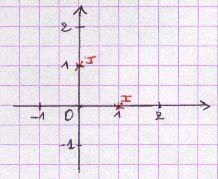
A’ est le symétrique de A par rapport à un point O signifie que O est le milieu de [AA’].

S 27

Notation : A’ = s_O (A).

Les symétries centrales conservent les distances, les aires, les angles, les milieux, l’alignement, le parallélisme et l’orthogonalité. 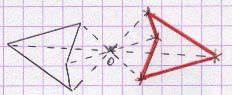S 28

Symétrie orthogonale :

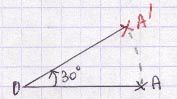
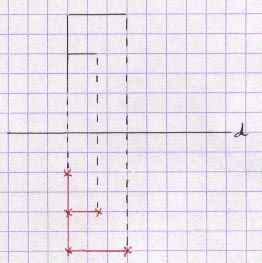
La symétrie orthogonale ou symétrie axiale est la transformation qui associe à un point ou à une figure son symétrique par rapport à une droite.

A’ est le symétrique de A par rapport à une droite d signifie que d est la médiatrice de [AA’].

S 29

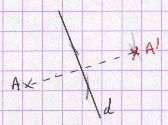
Notation : A’ = s_d (A).

Les symétries orthogonales conservent les distances, les aires, les angles, les milieux, l’alignement, le parallélisme et l’orthogonalité.

S 30

Symétrique :

Le symétrique d’un point ou d’une figure est l’image de ce point ou de cette figure par une symétrie centrale ou orthogonale.

Système décimal :

Le système décimal est un système dans lequel on utilise une numération décimale, basée sur dix chiffres (0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 et 9).

Ce système est le plus couramment utilisé dans le monde entier pour écrire nos nombres.

Système d’équations :

Un système de deux équations du premier degré à deux inconnues est constitué de deux égalités dans lesquelles il y a deux inconnues (à l’exposant 1).

Il est de la forme ax + by + c = 0 et a'x + b'y + c' = 0 (où a, b, c, a’, b’ et c’ sont des nombres fixés).

Exemple : 2x + 3y - 5 = 0 et 3x - 2y + 1 = 0.

Système d’inéquations :

Un système de deux inéquations du premier degré à une inconnue est constitué de deux inégalités dans lesquelles il y a une inconnue (à l’exposant 1).

Exemple : 2x - 1 ≤ 2 et x + 1 > 0.

Partager cet article

Repost0

Published by Jean-Luc ROMET - dans Maths en dico
commenter cet article …

15 février 2019 5 15 /02 /février /2019 13:39

Dictionnaire : de Simplification à Statistique

Simplification :

La simplification est l’action de simplifier une fraction.

Simplifier :

Simplifier une fraction, c’est la remplacer par une fraction égale dont le numérateur et le dénominateur sont plus petits (en restant entiers).

Exemple : 12 / 8 = (12 : 4) / (8 : 4) = 3 / 2.

Sinus d’un angle aigu :

Le sinus d’un angle aigu dans un triangle rectangle est le rapport de la longueur du côté opposé sur la longueur de l’hypoténuse.

Le sinus d’un angle aigu est un nombre sans unité compris entre 0 et 1.

sin 0° = 0 ; sin 30° = 1 / 2 ; sin 45° = √2 / 2 ; sin 60° = √3 / 2 ; sin 90° = 1.

S 15

Le sinus de l’angle EGF est noté sin EGF.

sin EGF = FG / EG.

Six :

Six est un chiffre qui s’écrit 6.

Exemple : Un dé contient six faces.

Soixante :

Soixante est un nombre qui s’écrit 60.

Exemple : L’âge de la retraite est en général soixante ans.

Soit :

Soit est un mot (verbe) qui sert à introduire les données de l’exercice.

Exemple : Soit A un point de la droite d.

Solide géométrique :

Un solide géométrique est une portion du plan limitée de toutes parts par une surface.

Les cônes de révolution, les cylindres de révolution, les prismes droits, les pyramides, les sphères, les pavés droits sont des solides géométriques.

Solution d’une équation :

Dans une équation à une inconnue x, une solution de l’équation est un nombre qui remplace x et qui est tel que l’égalité soit vraie.

Exemple : x + 3 = 8.

5 est solution de l’équation car 5 + 3 = 8.

Dans une équation à deux inconnues x et y, un couple (x ; y) est solution de l’équation si x et y ont des valeurs telles que l’égalité soit vraie.

Exemple : y = 2x + 3.

(5 ; 13) est solution de l’équation car 13 = 2 × 5 + 3.

Somme :

Une somme est le résultat d’une addition.

Exemple : 7 est la somme de 4 et de 3 car 7 = 4 + 3.

Somme des angles d’un triangle :

La somme des angles d’un triangle est égale à 180°.

α₁ + α₂ + α₃ = 180°.

S 16

Exemple : ABC est un triangle tel que α₁ = 50° et α₃ = 70°.

Calculons l’angle α₂ .

α₁ + α₂ + α₃ = 180°

50° + α₂ + 70° = 180°

α₂ = 180° - 50° - 70°

α₂ = 60°

Sommet :

Un sommet d’un polygone ou d’un solide géométrique est une extrémité d’un côté de ce polygone ou d’une arête de ce solide.

Un sommet d’un angle est le point commun aux deux côtés de l’angle.

S 19

Le cône n’a pas d’arête, mais a tout de même un sommet.

S 20

Une pyramide a plusieurs sommets, dont un sommet principal, celui qui n’appartient pas à sa base. S 21

Soustraction :

La soustraction est l’opération qui à deux nombres a et b associe leur différence a – b.

Exemple : 8 – 5 = 3.

Technique : S 22

donc, 53,24 – 2,16 = 51,08.

Soustraction des fractions :

Une soustraction de fractions est l’opération qui associe à deux fractions leur différence.

Pour effectuer une soustraction de fractions de même dénominateur, on conserve ce dénominateur et on soustrait les numérateurs.

Exemple : 11 / 3 - 4 / 3 = (11 - 4) / 3 = 7 / 3 .

Pour effectuer une soustraction de fractions de dénominateurs différents, on les réduit au même dénominateur et on applique la règle précédente.

Exemple : 5 / 4 - 3 / 2 = 5 / 4 - (3 × 2) / (2 × 2) = 5 / 4 - 6 / 4 = - 1 / 4 .

Soustraction des nombres relatifs :

Une soustraction de nombres relatifs est l’opération qui associe à deux nombres relatifs leur différence.

Pour effectuer une soustraction de deux nombres relatifs, on ajoute au premier l’opposé du second.

Si a et b sont des nombres relatifs, a – b = a + (– b).

Exemple : 7 – (- 3) = 7 + 3 = 10.

Sphère :

Une sphère de centre O et de rayon r est l’ensemble des points de l’espace situés à la distance r du point O. S 23

Statistique :

La statistique est la partie des mathématiques qui a pour but la collecte, l’analyse et l’interprétation d’observations relatives à des phénomènes collectifs.

Partager cet article

Repost0

Published by Jean-Luc ROMET - dans Maths en dico
commenter cet article …

19 octobre 2018 5 19 /10 /octobre /2018 19:59

Dictionnaire : de Seconde à Signe d'un nombre

Seconde :

Une seconde est une unité de mesure de temps.

Symbole : s.

Exemple : Une minute contient soixante secondes.

Secteur angulaire :

Un secteur angulaire est une des deux portions de plan limitée par deux demi-droites de même origine.

S 01

Secteur circulaire :

Un secteur circulaire est une des deux portions de disque limitée par deux rayons.

S 02

Section d’un cône par un plan :

La section d’un cône de révolution par un plan parallèle à sa base est un cercle qui est une réduction de sa base. S 03

Section d’un cylindre par un plan :

La section d’un cylindre de révolution par un plan parallèle à sa base est un cercle.

S 04

La section d’un cylindre de révolution par un plan perpendiculaire à sa base est un rectangle. S 05

Section d’un pavé droit par un plan :

La section d’un pavé droit (ou parallélépipède rectangle) par un plan parallèle à une arête ou à une face est un rectangle.

Section d’un solide par un plan :

La section d’un solide par un plan est une ligne ou une surface déterminée par la rencontre du solide et du plan.

Section d’une pyramide par un plan :

La section d’une pyramide par un plan parallèle à sa base est une réduction de sa base.

S 08

Section d’une sphère par un plan :

La section d’une sphère par un plan est un cercle.

S 09

Segment :

Un segment est une portion de droite limitée par deux points appelés extrémités.

S 10

Notation : [AB].

Segments adjacents :

Deux segments adjacents sont deux segments qui ont une extrémité commune et qui n’ont pas le même support. S 11

Les segments [EF] et [FG] sont adjacents.

Seize :

Seize est un nombre qui s’écrit 16.

Exemple : En huitième de finale d’un tournoi, il y a seize équipes présentes.

Sens de rotation :

Deux sens de rotation sont possibles :

- Le sens positif ou direct est le sens inverse de celui des aiguilles d’une montre.

- Le sens négatif est celui des aiguilles d’une montre.

S 12

Sens d’une demi-droite :

Pour une même direction, deux sens d’une demi-droite sont possibles :

S 13

- Les demi-droites [AB) et [AC) ont des sens opposés.

S 14

- Les demi-droites [EF) et [GH) ont même sens.

Sept :

Sept est un chiffre qui s’écrit 7.

Exemple : Une semaine a sept jours.

Série statistique :

Une série statistique est une liste de valeurs prises par un caractère étudié sur une population donnée.

Exemple : On peut étudier dans une classe la taille des élèves.

Signe d’un nombre :

Le signe d’un nombre est un symbole noté + ou – affecté à un nombre.

Le signe + est réservé aux nombres positifs.

Le signe – est réservé aux nombres négatifs.

Partager cet article

Repost0

Published by Jean-Luc ROMET - dans Maths en dico
commenter cet article …

23 février 2017 4 23 /02 /février /2017 08:55

Dictionnaire : de Repère à Rotation

Repère d’une droite :

Un repère d’une droite est un couple de points de la droite, le premier étant affecté du nombre 0, le second du nombre 1.

A partir de ce repère, on peut graduer une droite.

R 12

(O , I ) est un repère de la droite d.

Repère orthogonal :

Un repère orthogonal du plan est un triplet de trois points, le premier ayant les coordonnées (0 ; 0), le second les coordonnées (1 ; 0) et le troisième les coordonnées (0 ; 1). Les deux droites doivent être perpendiculaires. R 13

(O , I , J) est un repère orthogonal du plan.

Repère orthonormal :

Un repère orthonormal ou orthonormé est un repère orthogonal (O , I , J) tel que

OI = OJ = 1.

R 14

(O , I , J) est un repère orthonormal du plan.

Représentation graphique d’une fonction :

Une représentation graphique d’une fonction est une droite ou plus généralement une courbe tracée dans un repère du plan et associée à cette fonction.

La représentation graphique d’une fonction f est l’ensemble des points de coordonnées (x ; f(x)) lorsqu’on peut calculer f(x).

Ici, la géométrie permet d’illustrer une expression algébrique.

Exemple : Représentons graphiquement la fonction f telle que f(x) = 2x + 1.

La fonction f est affine, donc elle est représentée graphiquement par une

droite d_f d’équation y = 2x + 1.

Si x = 0 ; y = 2 × 0 + 1 = 0 + 1 = 1 ; f(x) = 1.

Si x = 1 ; y = 2 × 1 + 1 = 2 + 1 = 3 ; f(x) = 3.

Les points (0 ; 1) et (1 ; 3) appartiennent à la droite d_f .

R 15

Représentation graphique d’une série statistique :

Une représentation graphique d’une série statistique est un dessin qui illustre une série statistique.

Reproduire :

Reproduire exactement une figure plane, c’est construire une figure semblable en respectant ses dimensions.

Reproduire une figure à une échelle e, c’est faire une figure réduite (si 0 < e < 1) ou agrandie (si e > 1) en multipliant chacune des dimensions de la figure de départ par le nombre e.

Résolution :

La résolution est l’action de résoudre une équation ou une inéquation.

Résoudre une équation à deux inconnues :

Résoudre une équation à deux inconnues x et y, c’est déterminer les valeurs des couples
(x ; y) qui sont tels que l’égalité soit vraie.

Les solutions de l’ équation y = ax + b sont les couples (x ; y) tels que y = ax + b.

Exemple : Le couple (1 ; 5) est solution de l’équation y = 2x + 3 car 5 = 2 × 1 + 3.

Résoudre une équation à une inconnue :

Résoudre une équation à une inconnue x, c’est trouver, si elles existent, la ou les valeurs de l’inconnue x qui rendent vraie l’égalité.

Exemple : Résolvons x – 3 = 7.

x = 7 + 3

x = 10

10 est solution de l’équation x – 3 = 7.

L’équation x + a = b admet une solution unique x = b – a. (a et b sont des nombres fixés)

Exemple : Résolvons x + 3 = 1

x = 1 – 3

x = – 2

– 2 est solution de l’équation x + 3 = 1.

L’équation ax = b admet une solution unique x = b : a. (a et b sont des nombres fixés tels que
a ≠ 0)

Exemple : Résolvons 2 x = 6

x = 6 : 2

x = 3

3 est solution de l’équation 2 x = 6.

L’équation x² = a (a > 0) admet deux solutions √a et – √a.

L’équation x² = a (a < 0) n’admet pas de solution .

L’équation x² = 0 admet une solution x = 0.

Exemple : Résolvons x² = 5

√5 et – √5 sont les solutions de l’équation x² = 5.

L’équation-produit (ax + b)(cx + d) = 0 (où a, b, c et d sont des nombres fixés tels que a ≠ 0 et c ≠ 0) admet deux solutions qui sont – b : a et – d : c.

Exemple : Résolvons (2x – 1)(x + 2) = 0

Soit 2x – 1 = 0 Soit x + 2 = 0

2x = 1 x = – 2

x = 1 : 2

x = 0,5

0,5 et – 2 sont les solutions de l’équation (2x – 1)(x + 2) = 0.

Résoudre une inéquation à une inconnue :

Résoudre une inéquation à une inconnue x, c’est déterminer, si elles existent, les valeurs du terme inconnu x qui rendent vraie l’inégalité.

Exemple : Résolvons x – 1 ≤ 2

x ≤ 2 + 1

x ≤ 3

Les solutions de l’inéquation x – 1 ≤ 2 sont représentés par :

Résoudre un système de deux équations :

Résoudre un système de deux équations du type ax + by + c = 0 et a'x + b'y + c' = 0 (où a, b, c, a’, b’ et c’ sont des nombres fixés), c’est trouver, s’ils existent, le ou les couples (x ; y) qui rendent vraies simultanément les deux égalités.

Exposons deux méthodes de résolution :

La méthode par combinaison linéaire (ou par addition) :

On multiplie les équations de départ par deux nombres de façon qu’en ajoutant les nouvelles équations, on obtienne une équation du premier degré à une inconnue.

Exemple : Résolvons 2x - 3y + 10 = 0 (1) et x + y + 5 = 0 (2) par addition.

2x - 3y + 10 = 0 (1) × 1

x + y + 5 = 0 (2) × 3

2x - 3y + 10 = 0

3x + 3y + 15 = 0

addition des deux équations

5x + 25 = 0

5x = – 25

x = – 25 / 5

x = – 5

(2) x + y + 5 = 0

– 5 + y + 5 = 0

y = 5 – 5

y = 0

Le système d’équations admet une solution unique, le couple (– 5 ; 0).

La méthode par substitution :

A partir d’une des deux équations, on exprime une inconnue en fonction de l’autre. Dans la seconde équation, on remplace cette inconnue par ce qu’on vient d’obtenir de façon à se ramener à une équation du premier degré à une inconnue.

Exemple : Résolvons 2x - 3y + 10 = 0 (1) et x + y + 5 = 0 (2) par substitution.

(2) x + y + 5 = 0

y = – x – 5

(1) 2x – 3y + 10 = 0

2x – 3(– x – 5) + 10 = 0

2x + 3x + 15 + 10 = 0

2x + 3x = – 15 – 10

5x = – 25

x = – 25 / 5

x = – 5

(2) y = – x – 5

y = – (– 5) – 5

y = 5 – 5

y = 0

Le système d’équations admet une solution unique, le couple (– 5 ; 0).

Résoudre un système d’inéquations à une inconnue :

Résoudre un système d’inéquations à une inconnue, c’est trouver, si elles existent, la ou les valeurs de l’inconnue qui rendent vraies simultanément les deux inégalités.

Exemple : Résolvons x – 1 ≤ 2 (1) et 2x ≥ 4 (2).

(1) x – 1 ≤ 2 (2) 2x ≥ 4

x ≤ 2 + 1 x ≥ 4 : 2

x ≤ 3 x ≥ 2

Cherchons les solutions communes :

Les solutions de ce système sont les nombres x tels que 2 ≤ x ≤ 3.

Respectif :

Respectif ou respectivement signifie que l’on suit l’ordre d’énumération.

Exemple : I et J sont les milieux respectifs de [AB] et [AC] signifie que :

I est le milieu de [AB] et J est le milieu de [AC].

Reste :

Un reste est le nombre entier qui reste dans une division euclidienne.

R 19

r est le reste. r = a – b q. (r < b)

Exemple :

R 20

3 est le reste. 3 = 23 – 5 × 4.

Il existe aussi des restes dans des divisions non euclidiennes.

Retrancher :

Retrancher un nombre à un autre nombre, c’est le soustraire de cet autre nombre.

Exemple : Retrancher 3 à 7 donne 7 – 3 = 4.

Rotation :

La rotation est la transformation qui à un point A associe le point A’, image de A par la rotation de centre O et d’angle (– 180° < α° ≤ 180°).

Ce point est tel que angle AOA’ = α° et OA = OA’.

R 21

Les rotations conservent les distances, les aires, les angles, les milieux, l’alignement, le parallélisme et l’orthogonalité. R 22

Partager cet article

Repost0

Published by Jean-Luc ROMET - dans Maths en dico
commenter cet article …

8 février 2015 7 08 /02 /février /2015 10:53

Dictionnaire : de Racine carrée à Repérage

Racine carrée :

La racine carrée de a (a est un nombre positif), notée √a, est le nombre positif qui, multiplié par lui-même, donne a.

Exemples : √64 = 8 ; √2 ≈ 1,414.

a et b étant des nombres positifs, on a :

(√a)² = a ; √a × √b = √(a × b) ; √a / √b = √(a / b) (si b ≠ 0).

Exemples : √45 = √(9 × 5) = √9 × √5 = 3 × √5 = 3√5.

√(9 / 16) = √9 / √16 = 3 / 4 .

Radical :

Un radical est un symbole √ utilisé pour l’écriture des racines carrées.

Exemple : √25 = 5.

Raisonnement :

Un raisonnement est un enchaînement logique de phrases mathématiques (hypothèses, définitions, propriétés, opérations....) en vue d’obtenir une conclusion.

Dans un raisonnement déductif, chaque phrase mathématique induit la suivante.

En principe, on recherche d’abord les hypothèses, on indique la bonne propriété ou définition du cours et on en déduit la conclusion.

Exemple : ABC est un triangle isocèle en A,

d’après la propriété : si un triangle est isocèle, alors il a deux côtés de même

longueur,

AB = AC.

Rapport :

Le rapport de a sur b, noté a : b, est le quotient de a par b.

Exemples : Le rapport de 3 sur 5 est 3 : 5 = 0,6.

En Physique, la masse volumique est le rapport de la masse sur le volume.

Rapporteur :

Un rapporteur est un instrument semi-circulaire gradué généralement en degrés qui sert à mesurer ou à représenter des angles.

R 01

Rayon :

Un rayon d’un cercle est un segment qui relie le centre du cercle à un point du cercle.

R 02

[OA] est un rayon.

Un cercle a une infinité de rayons.

Le rayon d’un cercle désigne aussi la distance du centre du cercle à l’un des points du cercle.

Un rayon d’une sphère est un segment qui relie le centre de la sphère à un point quelconque de cette sphère. R 03

Le rayon d’une sphère désigne aussi la distance du centre de la sphère à l’un des points de la sphère.

Réciproque d’une propriété :

La réciproque d’une propriété est obtenue à partir de cette propriété de départ en inversant une hypothèse et la conclusion.

Exemple : Propriété : Si un point appartient à la médiatrice d’un segment, alors il est à

égale distance des extrémités de ce segment.

Propriété réciproque : Si un point est à égale distance des extrémités d’un

segment, alors il appartient à la médiatrice de ce segment.

La réciproque d’une propriété n’est pas toujours vraie.

Exemple : Si a = b, alors a² = b².

Par contre, si a² = b², on n’a pas forcément a = b (on peut avoir a = - b).

Réciproque du théorème de Pythagore :

La réciproque du théorème de Pythagore dit que si ABC est un triangle tel que

BC² = AB² + AC², alors le triangle ABC est rectangle en A.

R 04

Exemple : AB = 3 cm ; AC = 4 cm ; BC = 5 cm.

AB² = 9 ; AC² = 16 ; BC² = 25.

On a : 25 = 9 + 16

BC² = AB² + AC².

D’après la réciproque du théorème de Pythagore,

ABC est un triangle rectangle en A.

Réciproque du théorème de Thalès :

La réciproque du théorème de Thalès dit que si ABC est un triangle ; A, M et B sont alignés dans cet ordre ; A, N et C sont alignés dans cet ordre et AM / AB = AN / AC,

alors (MN) // (BC).

R 05

Exemple : AM = 1,2 cm ; AN = 2,1 cm ; AB = 1,6 cm ; AC = 2,8 cm.

AM / AB = 1,2 / 1,6 = 0,75 ; AN / AC = 2,1 / 2,8 = 0,75.

ABC est un triangle,

A, M et B sont alignés dans cet ordre,

A, N et C sont alignés dans cet ordre,

AM / AB = AN / AC.

D’après la réciproque du théorème de Thalès,

(MN) // (BC).

Réciproque du théorème des milieux :

La réciproque du théorème des milieux dit que dans un triangle, si une droite passe par le milieu d’un côté en étant parallèle au second côté, alors elle coupe le troisième côté en son milieu.

R 06

Exemple : Dans le triangle ABC,

I est le milieu de [AB],

La parallèle à (BC) passant par I coupe (AC) en J.

D’après la réciproque du théorème des milieux,

(IJ) // (BC).

Rectangle :

Un rectangle est un quadrilatère qui a quatre angles droits.

R 07

Propriétés caractéristiques :

- Si un quadrilatère a quatre angles droits, alors c’est un rectangle.

- Si un parallélogramme a deux côtés perpendiculaires, alors c’est un rectangle.

- Si un parallélogramme a ses diagonales de même longueur, alors c’est un rectangle.

Réduction d’une expression :

Une réduction d’une expression algébrique est l’action de réduire cette expression.

Réduction d’une figure ou d’un solide:

Une réduction d’une figure ou d’un solide géométrique est une reproduction de cette figure ou de ce solide à une échelle strictement inférieure à 1.

R 08

Si les dimensions d’une figure plane ou d’un solide sont multipliées par k (0 < k <1), alors les aires sont multipliées par k², les volumes sont multipliés par k³.

La petite pyramide est une

réduction de la grande.

Le petit cône est une

réduction du grand.

Réduire :

Réduire une expression algébrique, c’est regrouper ensemble les termes de même nature.

Exemples : 2x + 7 + 5x – 3 = 7x + 4.

(car 2x + 5x = 7x et + 7 – 3 = + 4)

5x² – 3x + 7x² – 8x = 12x² – 11x.

(car 5x² + 7x² = 12x² et – 3x – 8x = – 11x)

Réduire une figure géométrique, c’est la reproduire à une échelle plus petite.

Règle à calcul :

Une règle à calcul est un instrument qui permettait d’effectuer certains calculs assez rapidement. Elle était basée sur des fonctions que l’on étudie en classe de Terminale : les Logarithmes.

Règle de calcul :

Une règle de calcul est un nom donné à certains énoncés mathématiques en calcul numérique ou algébrique.

Exemple : Règle des signes :

- Le produit de deux nombres de même signe est un nombre positif.

- Le produit de deux nombres de signes différents est un nombre négatif.

5 × (– 7) = – 35 ; (– 3) × (– 4) = 12 ; – 8 × 2 = – 16 ; 4 × 6 = 24.

Règle de trois :

La règle de trois est une technique pour calculer le quatrième terme d’une proportion connaissant les trois autres.

Règle graduée :

Une règle graduée est un instrument qui sert à tracer des lignes droites et à mesurer des longueurs. R 11

Repérage :

Le repérage est l’action de repérer un point sur une droite graduée ou dans un plan.

Partager cet article

Repost0

Published by Jean-Luc ROMET - dans Maths en dico
commenter cet article …

15 juin 2014 7 15 /06 /juin /2014 08:04

Dictionnaire : de Quadrant à Quotient

Quadrant :

Un quadrant est une des quatre parties déterminées par un repère orthogonal dans un plan.

Q 01

Quadrilatère :

Un quadrilatère est un polygone qui a quatre côtés.

Q 02

A, B, C et D sont les sommets.

[AB], [BC], [CD] et [DA] sont les côtés.

[AC] et [BD] sont les diagonales.

Les trapèzes, les parallélogrammes, les rectangles, les losanges et les carrés sont des quadrilatères particuliers.

Quadrillage :

Un quadrillage est un ensemble de lignes qui divisent le plan en carrés.

Q 03

Quarante :

Quarante est un nombre qui s’écrit 40.

Exemple : Pour les catholiques, le carême dure quarante jours.

Quart :

Un quart est une partie d’un groupe partagé en quatre unités.

Quatorze :

Quatorze est un nombre qui s’écrit 14.

Exemple : A la belote, le neuf d’atout vaut quatorze points.

Quatre :

Quatre est un chiffre qui s’écrit 4.

Exemple : Un chien a quatre pattes.

Quatrième proportionnelle :

La quatrième proportionnelle est le quatrième terme d’une proportion dans laquelle on connaît les trois autres.

S₁	a	b
S₂	c	d

Dans le tableau de proportionnalité suivant,

on a l’égalité des produits en croix : a × d = b × c.

a, b, c et d sont quatre nombres non nuls.

On déduit : a = (b × c) : d ; b = (a × d) : c ; c = (a × d) : b ; d = (b × c) : a.

La technique de calcul était anciennement la « règle de trois ». Il y avait une variante dans la manière de disposer les calculs.

Exemple : 8 kg de pommes coûtent 10 €.

Calculons le prix de 5 kg de pommes.

masse de pommes (kg)	8	5
prix (€)	10	x

8 × x = 10 × 5

8 × x = 50

x = 50 / 8

x = 6,25

Le prix de 5 kg de pommes est 6,25 €.

Quintal :

Un quintal est une unité de mesure de masse équivalant à 100 kg.

Symbole : q.

Quinze :

Quinze est un nombre qui s’écrit 15.

Exemple : Au tournoi des six nations, les équipes de rugby ont quinze joueurs.

Quotient :

Un quotient est le résultat d’une division.

Un quotient euclidien est le quotient d’une division euclidienne.

Exemple : Q 06

6 est le quotient euclidien de 52 par 8.

Un quotient exact est le quotient lorsque le reste de la division est nul.

Exemple : Q 07

2,1 est le quotient exact de 10,5 par 5.

Lorsque le reste de la division n’est pas nul, on peut donner un quotient approché de la division.

Exemple : Q 08

20 : 11 ≈ 1,81.

1,81 est un quotient approché à 0,01 près de 20 par 11.

Partager cet article

Repost0

Published by Jean-Luc ROMET - dans Maths en dico
commenter cet article …

23 octobre 2013 3 23 /10 /octobre /2013 10:19

Dictionnaire : de Pourcentage à Pythagore

Pourcentage :

Un pourcentage est une proportion pour 100 unités.

Notation : p % = p / 100.

Appliquer p % à un nombre x, c’est effectuer le calcul (x × p) : 100.

Exemple : (80 × 20) : 100 = 1600 : 100 = 16.

20 % de 80 € représentent 16 €.

Déterminer le pourcentage de x éléments par rapport à y possibles, c’est effectuer le calcul

(x × 100) : y.

Exemple : Dans une classe de 25 élèves, 17 sont des filles.

(17 × 100) : 25 = 1700 : 25 = 68.

Le pourcentage de filles dans cette classe est 68 %.

Priorité des opérations :

La priorité des opérations permet de définir l’ordre dans lequel on doit effectuer ces opérations.

Les opérations prioritaires sont celles que l’on doit effectuer en premier. On a les règles suivantes :

- les calculs entre parenthèses sont prioritaires,

- en l’absence de parenthèses, les puissances sont prioritaires sur les multiplications et divisions qui elles mêmes sont prioritaires sur les additions et soustractions.

Exemples : Calculons A = 5 × (7 – 1) + 10 : (4 + 1)

A = 5 × 6 + 10 : 5

A = 30 + 2

A = 32.

B = 2³ × (5 + 1) + (- 1)⁵ × 25

B = 8 × (5 + 1) + (- 1) × 25

B = 8 ×6 + (- 1) × 25

B = 48 – 25

B = 23.

Prisme droit :

Un prisme droit est un solide constitué de deux bases qui sont des polygones superposables, les autres faces étant des rectangles.

P 40

Problème :

Un problème est une question à résoudre avec un raisonnement scientifique.

Produit :

Un produit est le résultat d’une multiplication

Exemple : 18 est le produit de 6 et de 3 car 6 × 3 = 18.

Produit en croix :

Dans une égalité a / b = c / d , on a l’égalité des produits en croix a × d = b × c.

Exemple : Comme 2 / 3 = 4 / 6, on a aussi 2 × 6 = 3 × 4 = 12.

S₁	a	b
S₂	c	d

Dans le tableau de proportionnalité ci-dessus, on a l’égalité des produits en croix : a × d = b × c.

Exemple :

masse de pommes (kg)	2	3
prix (€)	3,20	4,80

alors, 2 × 4,80 = 3,20 × 3.

Programme de calcul :

Un programme de calcul est une description de la suite de calculs que doit effectuer une personne ou un ordinateur.

Programme de construction :

Un programme de construction est une description de la suite de constructions géométriques que doit effectuer une personne ou un ordinateur.

Proportion :

Une proportion est un rapport de grandeur existant entre deux quantités.

Exemple : 30 élèves sur 50 ont réussi à un examen.

La proportion de réussite est 30 / 50 = 0,6 ou 60 %.

Proportionnalité :

La proportionnalité est la relation qu’ont entre elles deux suites proportionnelles.

Propriété :

Une propriété est une qualité particulière. Elle ne caractérise pas forcément la figure ou le nombre étudié.

Exemple : Si un quadrilatère est un rectangle, alors ses diagonales sont de même longueur.

(remarque : si un quadrilatère a uniquement ses diagonales de même

longueur, ce n’est pas forcément un rectangle)

Propriété caractéristique :

Une propriété caractéristique est une propriété qui détermine nettement un être mathématique.

Exemple : Si un parallélogramme a deux côtés perpendiculaires , alors c’est un rectangle.

Puissance :

La puissance nième d’un nombre a est : aⁿ = a × a × ……..× a (n fois)

(a est un nombre relatif, n un entier supérieur à 2).

aⁿ se dit « a puissance n » ou « a exposant n ».

Exemples : 5⁴ = 5 × 5 × 5 × 5 = 625 ; (- 2)³ = (- 2) × (- 2) × (- 2) = - 8.

a étant un nombre non nul, a¹ = a ; a⁰ = 1.

Exemple : 4⁰ = 1 ; 7¹ = 7.

a étant un nombre non nul et n un entier, a^{- n} = 1 / aⁿ .

Exemple : 4^-2 = 1 / 4² = 1 / 16 .

Avec les puissances, on a les propriétés suivantes :

pour a et b des nombres, n et p des entiers naturels,

aⁿ × a^p = aⁿ ^{+ p} ; aⁿ / a^p = aⁿ ^{– p} ; (a × b)ⁿ = aⁿ × bⁿ ; (aⁿ)^p = aⁿ ^{× p} .

Exemples : 3x² × 7x⁴ = 3 × 7 × x^{2 + 4} = 21 x⁶ ; 8 x⁵ / 2 x² = 8 / 2 x^{5 – 2} = 4 x³ ;

(2 x³)² = (2 × x³)² = 2² × (x³)² = 4x⁶ .

Puissance de 10 :

La puissance nième de 10 est : = 10 × 10 × ……..× 10 (n fois) = 100.........0 (n zéros)

(n un entier supérieur à 2).

On a : 10⁰ = 1 ; 10¹ = 10 ; 10^{- n} = = 0,00.........01 ; 10^{- 1} = 0,1.

Exemples : 10⁴ = 10000 ; 10^{- 3} = 0,001.

Avec les puissances de 10, on a les propriétés suivantes :

pour n et p des entiers naturels,

10ⁿ × 10^p = 10ⁿ ^{+ p} ; 10ⁿ / 10^p = 10ⁿ ^{- p} ; (10ⁿ)^p = 10ⁿ ^{× p} .

Exemples : On écrit sous forme décimale : 5 × 10³ × 3 × 10² = 15 × 10⁵ = 1 500 000.

On écrit sous forme scientifique : 8 × 10⁶ / 4 × 10² = 2 × 10⁴.

Pyramide :

Une pyramide est un solide géométrique constitué d’une base polygonale reliée à un sommet qui n’appartient pas au plan de base. P 41

Pyramide régulière :

Une pyramide régulière est une pyramide ayant comme base un polygone régulier, l’axe de ce polygone contenant le sommet de la pyramide.

Les arêtes latérales d’une pyramide régulière sont toutes de même longueur.

P 42

Pythagore :

Pythagore est un mathématicien grec né à Samos (570-480 avant J-C).

P 43

Il n’a laissé aucune trace écrite, sa vie et son oeuvre restent entourés de mystère.

Le célèbre théorème lié à son nom concernant l’hypoténuse d’un triangle rectangle nous parvient des Babyloniens, mais semble avoir été démontré par Pythagore.

Les Pythagoriciens formaient une secte scientifique, philosophique, apolitique et religieuse. Pour eux, les nombres sont la source de toute chose.

Pythagore a aussi travaillé sur l’arithmétique des entiers (table de Pythagore, nombres parfaits, nombres amicaux), les proportions et a énoncé d’autre théorèmes sur les triangles, les polygones, les cercles et les sphères.

Partager cet article

Repost0

Published by Jean-Luc ROMET - dans Maths en dico
commenter cet article …

14 juin 2013 5 14 /06 /juin /2013 10:18

Dictionnaire : de Perspective à Position d'une droite

Perspective cavalière :

La perspective cavalière permet de représenter sur un plan des solides de l’espace.

On utilise les conventions suivantes :

- Les lignes cachées sont en pointillé.

- Les lignes parallèles dans l’espace restent parallèles.

- Les droites perpendiculaires dans l’espace ne restent pas toujours perpendiculaires.

PGCD :

Le PGCD de deux nombres entiers, ou Plus Grand Commun Diviseur, est le plus grand des diviseurs communs à ces deux nombres.

Exemple : Prenons 16 et 20.

Les diviseurs de 16 sont : 1 ; 2 ; 4 ; 8 et 16.

Les diviseurs de 20 sont : 1 ; 2 ; 4 ; 5 ; 10 et 20.

Les diviseurs communs à 16 et 20 sont : 1 ; 2 et 4.

Le PGCD de 16 et 20 est 4.

Pour deux nombres premiers entre eux, le PGCD est 1.

Exemple : 9 et 13 sont premiers entre eux : leur seul diviseur commun est 1.

Le PGCD de 9 et 13 est 1.

Il existe une méthode pour déterminer le PGCD de deux nombres :

L’algorithme d’Euclide permet de calculer le PGCD de deux entiers naturels non nuls a et b sans avoir à dresser la liste des diviseurs de a et de b. a ≥ b.

On divise a par b, on obtient a = b × q₁ + r₁ .

si r₁ ≠ 0, on divise b par r₁, on obtient b = r₁ × q₂ + r₂ .

si r₂ ≠ 0, on divise r₁ par r₂, on obtient r₁ = r₂ × q₃ + r₃…….

On s’arrête quand le reste est nul.

Le PGCD de a et b est le dernier reste non nul.

Exemple : Calculer le PGCD de 420 et 1500.

Divisons 1500 par 420.

1500 = 420 × 3 + 240

420 = 240 × 1 + 180

240 = 180 × 1 + 60

180 = 60 × 3 + 0

Le PGCD de 420 et 1500 est 60.

Pi :

Le nombre Pi est le quotient du périmètre d’un cercle par son diamètre.

Symbole : π. π ≈ 3,14159.

Historiquement, les approximations du nombre π ont passionné les mathématiciens.

Avant notre ère, les Babyloniens trouvent que π ≈ 3.

Chez les Egyptiens, π ≈ 3 + 1/6, soit π ≈ 3,16.

Vers 250 ans avant J-C, Archimède, par la méthode des polygones inscrits et exinscrits à un cercle de rayon 1, arrive à une bonne approximation du nombre π. π ≈ 3,14.

Au début de notre ère, pour les Hindous, on arrive à π ≈ 3,1416.

Au 3^ème siècle, un Chinois parvient à déterminer que π ≈ 3,14159.

En 1593, un Français, François Viète donnera 11 décimales exactes.

Depuis 1706, on a des méthodes de calcul moins pénibles (on utilise des suites de calculs et on étudie leurs « limites »). On arrive ainsi à déterminer de nombreuses décimales de π (par exemple, le CEA à Paris a trouvé un million de décimales pour π).

La suite des décimales de π est utilisée pour tester le bon fonctionnement des ordinateurs.

Pied d’une hauteur :

Le pied d’une hauteur dans un triangle est le point d’intersection de la hauteur passant par un sommet et de la droite opposée à ce sommet. P 21 H est le pied de la hauteur issue de A dans le triangle ABC.

Plan :

Un plan est une surface plane illimitée.

Son image peut être la surface d’un lac ou une feuille de papier.

P 22

Notation : Plan (ABC).

Plans parallèles :

Deux plans parallèles sont deux plans qui n’ont pas de point commun ou qui sont confondus (égaux). P 23

Notation : P // P’.

Plans perpendiculaires :

Deux plans perpendiculaires sont deux plans sécants dont l’un d’eux contient une droite perpendiculaire à l’autre. P 24

Notation : P ^ P’.

Plans sécants :

Deux plans sécants sont deux plans dont l’intersection est une droite.

P 25

Point :

Un point est le plus petit élément de l’espace ou du plan.

Il est souvent représenté par une croix et se note avec une lettre majuscule.

Point de concours :

Un point de concours est un point commun à trois droites (ou plus de trois droites) concourantes. P 27

Point d’intersection :

Un point d’intersection est un point commun à deux droites sécantes.

P 28

Points cocycliques :

Des points cocycliques sont des points situés sur le même cercle.

P 29

Polyèdre :

Un polyèdre est un solide de l’espace limité par des polygones qu’on appelle des faces.

P 30

Les parallélépipèdes rectangles, les cubes, les pyramides et les prismes sont des polyèdres.

Un polyèdre ayant quatre faces s’appelle un tétraèdre.

Un polyèdre ayant huit faces s’appelle un octaèdre.

Polygone :

Un polygone est une ligne brisée fermée constituée de côtés.

Un polygone est aussi la surface limitée par cette ligne brisée fermée.

Les principaux polygones sont :

- le triangle (3 côtés),

- le quadrilatère (4 côtés),

- le pentagone (5 côtés),

- l’hexagone (6 côtés),

- l’heptagone (7 côtés),

- l’octogone (8 côtés),

- l’ennéagone (9 côtés),

- le décagone (10 côtés).

Polygone régulier :

Un polygone régulier est un polygone qui a tous ses côtés de même longueur et ses angles intérieurs de même mesure.

Polygones réguliers usuels :

triangle

équilatéral

carré

hexagone

régulier

octogone

régulier

P 37

La construction du pentagone régulier à la règle et au compas a longtemps passionné les mathématiciens.

Population statistique :

Une population statistique est un ensemble d’individus (hommes, animaux, objets divers...) soumis à une étude statistique.

Positif :

Un nombre positif est un nombre affecté d’un signe + ou sans signe.

Exemples : + 21 ; 589,7 ; ou √5.

Position d’une droite et d’un cercle :

La position relative d’une droite et d’un cercle dans un plan est la façon dont se rencontrent cette droite et ce cercle.

Il existe trois positions, une droite et un cercle peuvent avoir :

0 point commun :

1 point commun :

2 points communs :

La droite d₁ est

extérieure au cercle.

la droite d₂ est

tangente au cercle.

la droite d₃ est

sécante au cercle.

Partager cet article

Repost0

Published by Jean-Luc ROMET - dans Maths en dico
commenter cet article …

13 janvier 2013 7 13 /01 /janvier /2013 08:45

Dictionnaire : de Paire à Périmètre d'un rectangle

Paire :

Une paire est un ensemble de deux éléments.

Exemple : Une paire de chaussures est constituée de deux chaussures.

Papier millimétré :

Un papier millimétré est un quadrillage constitué de carrés d’un millimètre de côté, utilisé pour les tracés de graphiques qui exigent beaucoup de précision. P 01

Parallèle en géographie :

Un parallèle en géographie est un cercle imaginaire contenu dans la surface terrestre et dont le plan est parallèle au plan de l’équateur.

P 02

Parallélépipède rectangle :

Un parallélépipède rectangle ou pavé droit est un solide géométrique de l’espace constitué de six faces rectangulaires qui sont parallèles deux à deux.

P 03

Il a aussi huit sommets et douze arêtes.

Parallélogramme :

Un parallélogramme est un quadrilatère qui a ses côtés parallèles deux à deux.

P 04

Propriétés caractéristiques :

- Si un quadrilatère a ses côtés parallèles deux à deux, alors c’est un parallélogramme.

- Si un quadrilatère a ses diagonales qui ont le même milieu, alors c’est un parallélogramme.

Parenthèses :

Les parenthèses sont des symboles mathématiques représentés par ( et ) utilisés pour associer des nombres ou des lettres et pour indiquer des calculs prioritaires.

Exemple : Calculons 4(3x – 5) pour x = 2.

4(3x – 5) = 4 × (3 × 2 – 5) = 4 × (6 – 5) = 4 × 1 = 4.

Partager :

Partager, c’est diviser en plusieurs éléments.

P 05

Ce segment est partagé en quatre segments.

Partie décimale :

La partie décimale d’un nombre décimal est la partie située après la virgule.

Exemple : 36 est la partie décimale du nombre 548,36.

Partie entière :

La partie entière d’un nombre décimal est la partie située avant la virgule.

Exemple : 817 est la partie entière du nombre 817,041.

Pascal :

Blaise Pascal est un mathématicien, philosophe et physicien français du 17^ème siècle (1623-1662).

Pascal invente très jeune, à 19 ans, la première machine arithmétique permettant d’effectuer des additions et des soustractions à l’aide de simples mouvements de roue (la Pascaline).

P 06

Il a énormément fait progresser la géométrie en rédigeant un traité sur les coniques (courbe section d’un cône : ellipse, parabole ou hyperbole) et en organisant un concours sur les cycloïdes (étude du mouvement d’un point d’un cercle en train de rouler) au niveau mondial.

Pascal est certainement l’un des plus grands mathématiciens, son mysticisme et ses passions l’ont certainement empêché d’être encore plus productif. Il nous laisse tout de même une oeuvre assez considérable, dont les célèbres pensées.

Patron :

Un patron est un dessin qui permet par découpage, pliage et collage de réaliser un solide.

Patron d’un cube d’arête 1 cm :

P 07

Patron d’un parallélépipède rectangle de dimensions 1 cm, 2 cm et 2,5 cm :

P 08

Patron d’un cylindre de révolution de hauteur 2 cm et de rayon 1 cm :

P 09

Patron d’un prisme droit de hauteur 2 cm et de base un triangle équilatéral de côté 1 cm :

P 10

Patron d’une pyramide à base carrée de côté 1,5 cm et dont les faces latérales sont des triangles équilatéraux de côté 1,5 cm : P 11

Patron d’un cône de révolution de rayon r : P 12

Pavage :

Un pavage est un recouvrement d’une partie d’un plan ou d’un espace par des figures planes ou des solides identiques. P 13

Pentagone :

Un pentagone est un polygone qui a cinq côtés.


	Pentagone régulier

Périmètre :

Un périmètre est la longueur de la ligne qui délimite les contours d’une surface quelconque.

Périmètre d’un carré :

Le périmètre d’un carré de côté a est P = 4 × a .

P 16

4 × 3 = 12.

Le périmètre d’un carré de côté 3 cm est 12 cm .

Périmètre d’un polygone :

Le périmètre d’un polygone de dimensions a₁, a₂, ......, a_n est P = a₁ + a₂ + ...... + a_n .

P 17

2 + 4 + 5 + 9 + 8 = 28 .

Le périmètre d’un polygone de dimensions 2 cm ; 4 cm ; 5 cm ; 9 cm et 8 cm est 28 cm .

Périmètre d’un rectangle :

Le périmètre d’un rectangle de longueur L et de largeur l est P = 2 × (L + l).

P 18

2 × (6 + 4) = 2 × 10 = 20.

Le périmètre d’un rectangle de longueur 6 cm et de largeur 4 cm est 20 cm.

Partager cet article

Repost0

Published by Jean-Luc ROMET - dans Maths en dico
commenter cet article …

9 novembre 2012 5 09 /11 /novembre /2012 07:30

Dictionnaire : d'Octaèdre à Orthogonalité

Octaèdre :

Un octaèdre est un solide géométrique qui a huit faces.

Un octaèdre régulier a huit faces qui sont des triangles équilatéraux.

O 01

Octogone :

Un octogone est un polygone qui a huit côtés.

Il a aussi huit angles et huit sommets.


	Octogone régulier

Onze :

Onze est un nombre qui s’écrit 11.

Exemple : Une équipe de football a onze joueurs.

Opération :

Une opération est un calcul qui associe à deux nombres un autre nombre.

Les quatre opérations usuelles sont l’addition, la soustraction, la multiplication et la division. Il existe aussi les puissances.

Exemples : 8 + 2 = 10 ; 8 × 2 = 16 ; 8 – 2 = 6 ; 8 : 2 = 4 ;

8 ² = 64 ; 2 ⁸ = 256 .

Ordonnée :

L’ordonnée d’un point dans un repère est la deuxième des deux coordonnées qui caractérisent ce point.

Dans un repère orthogonal, l’ordonnée se lit sur l’axe vertical.

O 04

L’ordonnée de M est 1.

Ordonner :

Ordonner, c’est classer dans l’ordre croissant ou décroissant.

Exemple : Ordonnons avec le symbole < les nombres : 8 ; 3 ; 24 et 11.

3 < 8 < 11 < 24.

Ordre :

Un ordre est une disposition de nombres utilisant les symboles <, >, ≤ ou ≥.

Propriétés :

Si a < b et b < c, alors a < c.

Exemple : 2 < 5 et 5 < 9, alors 2 < 9.

L’addition et la soustraction conservent l’ordre :

Si a < b, alors a + c < b + c et a – c < b – c.

Exemple : 2 < 3, alors 2 + 7 < 3 + 7 et 2 – 1 < 3 – 1.

La multiplication par un nombre strictement positif conserve l’ordre :

Si a < b (et c > 0), alors a × c < b × c.

Exemple : 3 < 10, alors 3 × 5 < 10 × 5.

La multiplication par un nombre strictement négatif inverse l’ordre :

Si a < b (et c < 0), alors a × c > b × c.

Exemple : 7 < 15, alors 7 × (- 2) > 15 × (- 2).

Ordre croissant :

L’ordre croissant est l’ordre du plus petit au plus grand.

On utilise les symboles < ou ≤.

< signifie : est strictement inférieur à.

≤ signifie : est inférieur ou égal à.

Exemple : 5 < 10 < 104.

Ordre décroissant :

L’ordre décroissant est l’ordre du plus grand au plus petit.

On utilise les symboles > ou ≥.

> signifie : est strictement supérieur à.

≥ signifie : est supérieur ou égal à.

Exemple : 83 > 57 > 4.

Ordre de grandeur :

Un ordre de grandeur d’un nombre est une valeur approchée simple de celui-ci.

Exemple : A = 9 982 + 507. Donnons un ordre de grandeur de A.

9 982 est proche de 10 000 ; 507 est proche de 500.

Un ordre de grandeur de A est 10 000 + 500 = 10 500.

En faisant une opération, il est toujours possible de vérifier si on fait une erreur importante en évaluant un ordre de grandeur du résultat.

Orienté :

Une droite est orientée lorsqu’on lui attribue un sens.

Cette droite orientée est alors appelée axe.

O 05

Origine :

L’origine d’un axe est le point d’abscisse 0.

O 06

L’origine d’un repère est le point d’intersection des deux axes.

Ses coordonnées sont (0 ; 0).

O 07

Orthocentre :

L’orthocentre d’un triangle est le point de concours des trois hauteurs de ce triangle.

O 08

Orthogonalité :

L’orthogonalité est la qualité des éléments géométriques (droites, plans) qui sont orthogonaux.

Partager cet article

Repost0

Published by Jean-Luc ROMET - dans Maths en dico
commenter cet article …

MATHS-ROMETUS

Rechercher

Recherche

Rometus Champion

Archives

Rometus et histoire

Dictionnaire : de Stère à Système d'inéquations

Dictionnaire : de Simplification à Statistique

Dictionnaire : de Seconde à Signe d'un nombre

Dictionnaire : de Repère à Rotation

Dictionnaire : de Racine carrée à Repérage

Dictionnaire : de Quadrant à Quotient

Dictionnaire : de Pourcentage à Pythagore

Dictionnaire : de Perspective à Position d'une droite

Dictionnaire : de Paire à Périmètre d'un rectangle

Dictionnaire : d'Octaèdre à Orthogonalité

Articles RÉCents

Rometus toujours

Catégories

Rometus et blagues

Liens

Rometus en folie

MATHS-ROMETUS

Rechercher

Recherche

Rometus Champion

Archives

Rometus et histoire

Articles RÉCents

Rometus toujours

Catégories

Newsletter Du Blog

Rometus et blagues

Liens

Rometus en folie