Pourcentage :
Un pourcentage est une proportion pour 100 unités.
Notation : p % = p / 100.
Appliquer p % à un nombre x, c’est effectuer le calcul (x × p) : 100.
Exemple : (80 × 20) : 100 = 1600 : 100 = 16.
20 % de 80 € représentent 16 €.
Déterminer le pourcentage de x éléments par rapport à y possibles, c’est effectuer le calcul
(x × 100) : y.
Exemple : Dans une classe de 25 élèves, 17 sont des filles.
(17 × 100) : 25 = 1700 : 25 = 68.
Le pourcentage de filles dans cette classe est 68 %.
Priorité des opérations :
La priorité des opérations permet de définir l’ordre dans lequel on doit effectuer ces opérations.
Les opérations prioritaires sont celles que l’on doit effectuer en premier. On a les règles suivantes :
- les calculs entre parenthèses sont prioritaires,
- en l’absence de parenthèses, les puissances sont prioritaires sur les multiplications et divisions qui elles mêmes sont prioritaires sur les additions et soustractions.
Exemples : Calculons A = 5 × (7 – 1) + 10 : (4 + 1)
A = 5 × 6 + 10 : 5
A = 30 + 2
A = 32.
B = 23 × (5 + 1) + (- 1)5 × 25
B = 8 × (5 + 1) + (- 1) × 25
B = 8 ×6 + (- 1) × 25
B = 48 – 25
B = 23.
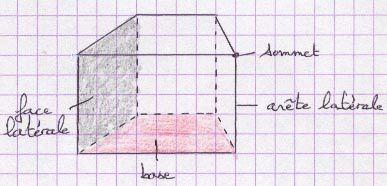
Prisme droit :
Un prisme droit est un solide constitué de deux bases qui sont des polygones superposables, les autres faces étant des rectangles.
Problème :
Un problème est une question à résoudre avec un raisonnement scientifique.
Produit :
Un produit est le résultat d’une multiplication
Exemple : 18 est le produit de 6 et de 3 car 6 × 3 = 18.
Produit en croix :
Dans une égalité a / b = c / d , on a l’égalité des produits en croix a × d = b × c.
Exemple : Comme 2 / 3 = 4 / 6, on a aussi 2 × 6 = 3 × 4 = 12.
| S1 | a | b |
| S2 | c | d |
Dans le tableau de proportionnalité ci-dessus, on a l’égalité des produits en croix : a × d = b × c.
Exemple :
| masse de pommes (kg) | 2 | 3 |
| prix (€) | 3,20 | 4,80 |
alors, 2 × 4,80 = 3,20 × 3.
Programme de calcul :
Un programme de calcul est une description de la suite de calculs que doit effectuer une personne ou un ordinateur.
Programme de construction :
Un programme de construction est une description de la suite de constructions géométriques que doit effectuer une personne ou un ordinateur.
Proportion :
Une proportion est un rapport de grandeur existant entre deux quantités.
Exemple : 30 élèves sur 50 ont réussi à un examen.
La proportion de réussite est 30 / 50 = 0,6 ou 60 %.
Proportionnalité :
La proportionnalité est la relation qu’ont entre elles deux suites proportionnelles.
Propriété :
Une propriété est une qualité particulière. Elle ne caractérise pas forcément la figure ou le nombre étudié.
Exemple : Si un quadrilatère est un rectangle, alors ses diagonales sont de même longueur.
(remarque : si un quadrilatère a uniquement ses diagonales de même
longueur, ce n’est pas forcément un rectangle)
Propriété caractéristique :
Une propriété caractéristique est une propriété qui détermine nettement un être mathématique.
Exemple : Si un parallélogramme a deux côtés perpendiculaires , alors c’est un rectangle.
Puissance :
La puissance nième d’un nombre a est : an = a × a × ……..× a (n fois)
(a est un nombre relatif, n un entier supérieur à 2).
an se dit « a puissance n » ou « a exposant n ».
Exemples : 54 = 5 × 5 × 5 × 5 = 625 ; (- 2)3 = (- 2) × (- 2) × (- 2) = - 8.
a étant un nombre non nul, a1 = a ; a0 = 1.
Exemple : 40 = 1 ; 71 = 7.
a étant un nombre non nul et n un entier, a- n = 1 / an .
Exemple : 4-2 = 1 / 42 = 1 / 16 .
Avec les puissances, on a les propriétés suivantes :
pour a et b des nombres, n et p des entiers naturels,
an × ap = an + p ; an / ap = an – p ; (a × b)n = an × bn ; (an)p = an × p .
Exemples : 3x2 × 7x4 = 3 × 7 × x2 + 4 = 21 x6 ; 8 x5 / 2 x2 = 8 / 2 x5 – 2 = 4 x3 ;
(2 x3)2 = (2 × x3)2 = 22 × (x3)2 = 4x6 .
Puissance de 10 :
La puissance nième de 10 est : = 10 × 10 × ……..× 10 (n fois) = 100.........0 (n zéros)
(n un entier supérieur à 2).
On a : 100 = 1 ; 101 = 10 ; 10- n = = 0,00.........01 ; 10- 1 = 0,1.
Exemples : 104 = 10000 ; 10- 3 = 0,001.
Avec les puissances de 10, on a les propriétés suivantes :
pour n et p des entiers naturels,
10n × 10p = 10n + p ; 10n / 10p = 10n - p ; (10n)p = 10n × p .
Exemples : On écrit sous forme décimale : 5 × 103 × 3 × 102 = 15 × 105 = 1 500 000.
On écrit sous forme scientifique : 8 × 106 / 4 × 102 = 2 × 104.
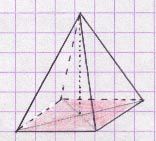
Pyramide :
Une pyramide est un solide géométrique constitué d’une base polygonale reliée à un sommet qui n’appartient pas au plan de base. 
Pyramide régulière :
Une pyramide régulière est une pyramide ayant comme base un polygone régulier, l’axe de ce polygone contenant le sommet de la pyramide.
Les arêtes latérales d’une pyramide régulière sont toutes de même longueur.
Pythagore :
Pythagore est un mathématicien grec né à Samos (570-480 avant J-C).

Il n’a laissé aucune trace écrite, sa vie et son oeuvre restent entourés de mystère.
Le célèbre théorème lié à son nom concernant l’hypoténuse d’un triangle rectangle nous parvient des Babyloniens, mais semble avoir été démontré par Pythagore.
Les Pythagoriciens formaient une secte scientifique, philosophique, apolitique et religieuse. Pour eux, les nombres sont la source de toute chose.
Pythagore a aussi travaillé sur l’arithmétique des entiers (table de Pythagore, nombres parfaits, nombres amicaux), les proportions et a énoncé d’autre théorèmes sur les triangles, les polygones, les cercles et les sphères.




















