Coordonnées d’un point :
Les coordonnées d’un point dans un repère du plan sont les deux nombres qui caractérisent la position du point dans le repère. 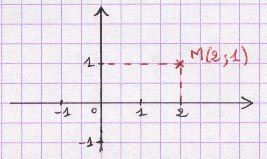
2 est l’abscisse de M. 1 est l’ordonnée de M.
Notation : M (x ; y) signifie que M a pour coordonnées x et y.
Coordonnées d’un vecteur :
Les coordonnées d’un vecteur dans un repère du plan sont les deux nombres qui caractérisent ce vecteur. 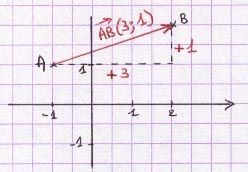
Notation : vecteur AB (x ; y) signifie que vecteur AB a pour coordonnées x et y.
Si A (xA ; yA) et B (xB ; yB), alors vecteur AB (xB - xA ; yB - yA) .
Exemple : si A (2 ; 4) et B (5 ; 3),
alors vecteur AB (5 – 2 ; 3 – 4), donc vecteur AB (3 ; -1) .
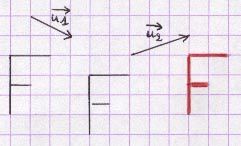
Coordonnées de la somme de deux vecteurs :
Les coordonnées de la somme de deux vecteurs s’obtiennent en ajoutant respectivement les coordonnées des deux vecteurs.
Si vecteur AB (x ; y) et vecteur CD (x’ ; y’) ,
alors vecteur AB + vecteur CD (x + x’ ; y + y’) .
Exemple : si vecteur AB (4 ; 3) et vecteur CD (1 ; 4) ,
alors vecteur AB + vecteur CD (5 ; 7) .
Coordonnées du milieu d’un segment :
Les coordonnées du milieu d’un segment s’obtiennent en effectuant la demi-somme des coordonnées respectives des deux extrémités du segment.
Si A (xA ; yA) ; B (xB ; yB) ; I (xI ; yI) ; I est le milieu de [AB],
alors, xI = (xA + xB) : 2 et yI = (yA + yB) : 2 .
Exemple : si A (3 ; 4) ; B (5 ; 2) et I est le milieu de [AB],
(3 + 5) : 2 = 8 : 2 = 4 et (4 + 2) : 2 = 6 : 2 = 3, donc I (4 ; 3).
Corde :
Une corde est un segment reliant deux points distincts d’un cercle. 
Cosinus d’un angle aigu :
Le cosinus d’un angle aigu dans un triangle rectangle est égal au rapport de la longueur du côté adjacent sur la longueur de l’hypoténuse.
Le cosinus d’un angle aigu est un nombre sans unité compris entre 0 et 1.
cos 30° = √3 / 2 ; cos 45° = √2 / 2 ; cos 60° = 1 / 2.

Notation : cos ABC signifie cosinus de l’angle ABC.
Dans le dessin, cos ABC = AB / BC.
Côté adjacent :
Le côté adjacent à un angle aigu dans un triangle rectangle est celui, en dehors de l’hypoténuse, qui borde cet angle aigu. 
Côté d’un polygone :
Un côté d’un polygone est un segment reliant deux sommets consécutifs d’un polygone.
Côté opposé :
Le côté opposé à un angle aigu dans un triangle rectangle est celui qui ne borde pas cet angle aigu.

Couple :
Un couple de nombres est formé par deux nombres associés dans un ordre.
Exemple : (4 ; 5) ≠ (5 ; 4) .
Un couple de points A et B est formé par deux points associés dans un certain ordre. Il est appelé bipoint (A ; B) .
Couronne circulaire :
Une couronne circulaire est une surface plane comprise entre deux cercles concentriques.

Critère de divisibilité :
Un critère de divisibilité est une propriété qui permet de reconnaître si un entier naturel est divisible par un autre entier naturel.
- Un entier est divisible par 2 s’il est pair.
- Un entier est divisible par 3 si la somme de ses chiffres est un multiple de 3.
- Un entier est divisible par 5 s’il se termine par 0 ou 5.
- Un entier est divisible par 9 si la somme de ses chiffres est un multiple de 9.
- Un entier est divisible par 10 s’il se termine par 0.
- Un entier est divisible par 11 si la différence entre la somme de ses chiffres de rangs impairs et la somme de ses chiffres de rangs pairs est divisible par 11.
- Un entier est divisible par 100 s’il se termine par 00.
Cube :
Un cube est un parallélépipède rectangle ayant 6 faces carrées.

Un cube a 8 sommets, 12 arêtes et 6 faces. Ses arêtes sont toutes de même longueur.
Cube d’un nombre :
Le cube d’un nombre a est a3 = a × a × a.
Le cube d’un nombre est toujours du même signe que ce nombre.
Exemples : Le cube de 2 est 2 × 2 × 2 = 8.
Le cube de (-1) est (-1) ×(-1) ×(-1) = - 1.
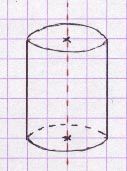
Cylindre de révolution :
Un cylindre de révolution est un solide engendré par un rectangle qui tourne autour de l’un de ses côtés.
Il a deux bases superposables qui sont des disques de même axe.